Pular para o conteúdo principal

Função Degrau Unitário

Função Degrau Unitário


O que é ?


A função degrau unitário (ou função de Heaviside) é muito utilizada na disciplina de Sinais e Sistemas Lineares e em análise de circuitos elétricos. Normalmente esta função é representada pela letra "u", e é dependente do tempo. Para valores de tempo menor que 0, a função vale 0, já para valores maiores ou iguais a 0, ela vale 1.  Podendo ser representada

Pra que serve ? 


Podemos usar a função degrau unitário para limitar o intervalo de outra função. Se tivermos um sinal y(t), como mostrado abaixo


Gráfico 1.


 e quisermos que ele inicie-se no tempo zero, então y(t) deve ser multiplicada por u(t). 


Gráfico 2.


Outra aplicação é para a representação de certas funções em termos de u(t). Isso pode ser conseguido com a manipulação da variável independente, no caso o tempo, manipulação da função u(t) além da combinação de diferentes funções degrau. Alguns exemplos se encontram logo abaixo

Gráfico 3.

Gráfico 4.

Gráfico 5.

Como usar no SciLab ?


Programa que cria a função u(t).
Agora vamos ver como é possível definir e trabalhar com a função u(t) no Scilab. Uma forma é construindo uma function, e salvando com a extensão sci. É bom lembrar que arquivos .sci devem ser carregados previamente (F5, função exec ou diretamente no botão Executar).
Para verificar se a nossa  function funciona corretamente e se ela realmente representa a função u(t), vamos criar outro programa, agora com a extensão .sce, para gerar um gráfico. O intervalo de tempo será entre -100 e 100, com passo de 0.01. Também iremos redimensionar os eixos (coma função mtlb_axis()) para uma melhor visualização do resultado.


Programa que plota a função u(t).

Gráfico 6.

Outra forma mais interessante de criarmos a função degrau é usando a função " deff ", do SciLab. Essa função possuí basicamente a seguinte sintaxe


Como observação, no espaço escrito "comandos", deve ser incluído um conjunto de strings que represente uma sequência de instruções.
Com a função u(t) definida dessa forma, foram criados os gráfico 3, 4 e 5, onde tanto a variável " t ", quanto a função u(t) foram manipuladas. Então, para criar essas figuras, basta seguir o exemplo da figura ao lado. A função funcprot foi usada porque anteriormente, u(t) havia sido definida de outra forma. A variável tempo é um vetor com valor inicial -2 e valor final 2, tendo um incremento de 0.01. As variáveis "a" e "c" são inicialmente matrizes booleanas, ou seja, contém apenas "T" - true- ou "F" - false. A função bool2s converte a matriz booleana em uma matriz com zeros e uns, o que permite que elas sejam plotadas. A função scf atribui, nesse caso, o valor 4 à janela gráfica criada. clf é função que limpa a janela gráfica e plot produz o gráfico.


Os gráficos gerados nesta postagem podem ser reproduzidos com os seguintes programas

Programa principal com extensão .sce.

Função com extensão .sci.

Scripts testados com: Scilab 5.5.2 (64-bit)
                                       Scilab 6.0.0 (64-bit)*


* Nessa versão, tanto a plotagem quanto outras operações que envolviam a função u(t) definida por uma "function", apresentaram problemas, como mensagens de erro e elevado tempo de execução das instruções.

P.S.: Colocar a manipulação de u(t) diretamente na função plot, por exemplo, plot(t, u(t-1)), pode gerar ou não o gráfico. Isso vai depender do que é feito com a função. 

Marcadores:
Local: Brasil

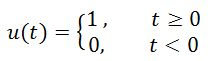
Comentários

Postar um comentário

Postagens mais visitadas deste blog

Critério de Estabilidade de Routh-Hurwitz

Critério de Estabilidade de Routh-Hurwitz Em uma outra postagem foi apresentado o critério de polos e zeros para verificar a estabilidade de um sistema. Na mesma linha de análise, temos também o critério de estabilidade de Routh-Hurwitz, que é explicado na sequência. O que é ? "Na teoria dos sistemas de controle , o critério de estabilidade de Routh-Hurwitz é um teste matemático que é uma condição necessária e suficiente para a estabilidade de um sistema de controle linear e invariante no tempo (LTI). O teste de Routh é um algoritmo recursivo eficiente que o matemático inglês Edward John Routh propôs em 1876 para determinar se todas as raízes do polinômio característico de um sistema linear apresentam partes reais negativas. O matemático alemão Adolf Hurwitz propôs de forma independente, em 1895, organizar os coeficientes do polinômio em uma matriz quadrada, chamada de matriz de Hurwitz, e mostrou que o polinômio é estável se, e somente se, a sequência dos determinantes de...
Postar um comentário
Leia mais

Polos e Zeros - Função plzr()

Polos e Zeros O que é ? Figura 1. Antes de falarmos de polos e zeros, vamos começar pela definição de função de transferência (FT). Temos que, a FT de um sistema linear nada mais é do que a relação entre a transformada de Laplace   da variável de saída com a transformada de Laplace da variável de entrada. Vale lembrar que as condições iniciais devem ser zero.    Figura 2. A FT do sistema representado no diagrama da figura 1 é a função G(s) (figura 2), em que a variável s (minúsculo) é chamada de frequência complexa. S(s) e E(s) são polinômios. E(s) é chamado de polinômio característico do sistema, sendo o grau n-ésimo desse polinômio  a ordem do sistema. Agora vamos as definições de polos e zeros. Polos: S ão os valores de s, de E(s) de uma função de transferência, que fazem com que a FT se torne infinita . Em outras palavras, são as raízes de E(s) = 0  Zeros: São  os valores de s, de S(s) de uma função de transferência, que fazem com ...
Postar um comentário
Leia mais