Critério de Estabilidade de Routh-Hurwitz

Critério de Estabilidade de Routh-Hurwitz

Em uma outra postagem foi apresentado o critério de polos e zeros para verificar a estabilidade de um sistema. Na mesma linha de análise, temos também o critério de estabilidade de Routh-Hurwitz, que é explicado na sequência.

O que é ?

"Na teoria dos sistemas de controle , o critério de estabilidade de Routh-Hurwitz é um teste matemático que é uma condição necessária e suficiente para a estabilidade de um sistema de controle linear e invariante no tempo (LTI). O teste de Routh é um algoritmo recursivo eficiente que o matemático inglês Edward John Routh propôs em 1876 para determinar se todas as raízes do polinômio característico de um sistema linear apresentam partes reais negativas. O matemático alemão Adolf Hurwitz propôs de forma independente, em 1895, organizar os coeficientes do polinômio em uma matriz quadrada, chamada de matriz de Hurwitz, e mostrou que o polinômio é estável se, e somente se, a sequência dos determinantes de suas submatrizes principais é positiva. Os dois procedimentos são equivalentes, com o teste de Routh fornecendo uma maneira mais eficiente de calcular os determinantes de Hurwitz do que informá-los diretamente. Um polinômio que satisfaz o critério de Routh-Hurwitz é chamado de polinômio de Hurwitz."(Wikipedia - Traduzido) [1].

Pra que serve ?

Este método é muito útil quando se tem no denominador de uma função de transferência (FT) um parâmetro desconhecido. Nesse caso é inviável, por meio de uma calculadora, determinar uma faixa de valores para esse parâmetro,  de tal modo que o sistema seja estável. Ao usar o critério de Routh-Hurwitz, conseguimos  encontrar uma expressão para a faixa de valores do parâmetro desconhecido.
  

Como faz ?

Inicialmente, vamos considerar a FT da figura 1, que representa uma função de transferência equivalente em malha fechada de um sistema.

Figura 1.

Como o que importa para determinar a estabilidade de um sistema são os polos, vamos voltar nossa atenção para o denominador. Usando o polinômio do denominador da função transferência da figura 1 construímos a tabela de Routh (Figura 2). 

Inicialmente, na primeira coluna, distribuímos de cima para baixo, as potências de "s", sempre da maior para a menor. Agora, observe que o elemento que está na primeira linha e primeira coluna, "s" está elevado à 5 (que é um número ímpar), então nas colunas seguintes desta linha devemos colocar os coeficientes com índice ímpar. Na linha 2, "s" está elevado a 4 (número par), logo preenchemos as colunas seguintes desta linha com os coeficientes que têm índice par.

Os demais elementos são uma divisão, onde o denominador é o primeiro elemento da linha anterior (fixo para todos os elementos dessa linha). O numerador é o negativo do determinante das entradas das linhas anteriores, onde a primeira coluna é sempre a primeira coluna anterior; já a segunda coluna segue a sequência das próximas colunas. Acrescente zero se necessário. A tabela está completa quando todas as linhas estiverem completas até S°. 

  

Figura 2.

De acordo com o critério de Routh-Hurwitz,  o número de raízes do polinômio que estão no semiplano direito é igual ao número de mudanças de sinal na primeira coluna. Se a FT em malha fechada tem todos os polos no lado esquerdo do plano s, o sistema é estável. Logo, um sistema é estável quando não há mudança de sinal na primeira coluna da tabela de  Routh-Hurwitz.

Como exemplo, considere o sistema apresentado na Figura 3. Determine o valor de K para que o sistema seja estável, instável ou marginalmente estável. Considere K > 0.

Figura 3.

  

 Solução

A tabela de Routh é construida como apresentado na Figura 4.

Figura 4.

Vamos a análise da tabela:

• Se K > 1386, teremos uma mudança de sinal por causa da terceira linha, gerando um sistema instável;

• Se K < 1386, todos os termos da primeira coluna serão positivos, não havendo mudança de sinal. Assim, o sistema será estável;

• Se K = 1386, teremos a terceira linha como nula. Isso leva à necessidade de voltar à linha anterior, derivar seu polinômio e considerá-lo assim (considerando K=1386). 

Nesse último caso, como não há mudanças de sinal do polinômio par (linha s2) para baixo, o polinô-mio par tem suas duas raízes no eixo imaginário apenas (do contrário, por simetria, haveria raízes no semiplano direito). Como não há mudanças de sinal acima do polinômio par também, as raízes res-tantes estão no semiplano esquerdo. Logo, o sistema é marginalmente estável. 

Como usar no SciLab ?

A função routh_t tem a seguinte sintaxe:

 

r=routh_t(h [,k])

Parâmetros

• h : Matriz quadrada de razões dos polinômios. Variável que armazena o polinômio.
• k: Ganho do sistema.

Exemplo

 Código

Console

Repare que a segunda linha (que contém os valores 10 e 1030) poderia ter sido multiplicada pelo fator 1/10, para fins de simplificação. Mas isso não impede a interpretação de que o sistema é instável pela mudança de sinal.  Agora veremos como a função se comporta em casos especiais da tabela.

• A tabela de Routh tem zero apenas na primeira coluna de uma linha 

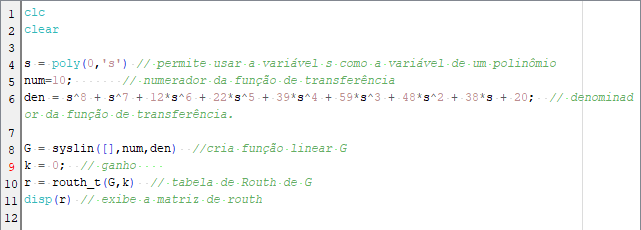
O Código

 O Console

Note que o Scilab utilizou a variável eps (que representa um valor muito pequeno).
  

• A tabela de Routh tem uma linha composta somente com zeros
  

O Código

 

O Console

 

Até essa parte, a função é executada da mesma forma que o cálculo manual. Após, uma sucessão de erros ocorre, então nesse caso não vale apena utilizar a função routh_t(). 

Referências

[1] Wikipedia. Routh–Hurwitz stability criterion. 2017. Disponível em: <https://en.wikipedia. org / wiki/Routh–Hurwitz_stability_criterion>. Acesso em: 02/10/2017.

Scripts testados com: Scilab 6.0.1 (64-bit)