Pular para o conteúdo principal

Frações Parciais

Frações Parciais

O que é ?

Figura 1.
Quando temos uma função racional (Figura 1), ou seja, uma razão entre polinômios, po- demos utilizar uma ferramenta matemática para expressar essa função como a soma de frações mais simples (conhecidas como frações parciais ou frações ele-mentares). Como o exemplo da Figura 2.

Figura 2.

As funções racionais podem ser classificadas nas seguintes categorias:

  • Função Racional Própria: É quando o grau do polinômio do numerador é inferior ao grau do polinômio do denominador. Por exemplo:
Figura 3.
  • Função Racional Imprópria: É a função racional, cujo grau do numerador não é menor que o do denominador, ou seja, ele é maior ou igual, por exemplo:
                                                     
                                                                      Figura 4.
Figura 5.

Exitem técnicas específicas, de expansão em frações parciais, para cada tipo de função racional, que só se aplicam a um ou a outro tipo.


Pra que serve ?


Esta técnica é utilizada no cálculo e em outras matérias para facilitar a integração de funções desse tipo (funções racionais). O cálculo de transformadas, principalmente transformadas inversas, de Fourier, de Laplace e Z, são mais facilmente executadas se utilizarmos esse recurso matemático.

Como fazer no SciLab ?


A função no Scilab que realiza a expansão em frações parciais é a pfss(), mas antes de usa-la é preciso definir a função racional (FR), temos como referência o programa abaixo. Com o auxílio da função poly(), definimos a variável dependente, no caso, "x" (linha 0014). Na sequência, construímos a FR normalmente (linha 0015), e a armazenamos em uma variável. Por fim, colocamos a variável com a FR como entrada da função pfss() (linha 0016).

Figura 6.

Figura 7.

A Figura 7 apresenta o script do programa principal, já a Figura 8 exibe o resultado da expansão em frações parciais para as FT alocadas nas variáveis A e B.

Função pfss (decomposição em frações parciais)


Na figura 8 encontra-se a sintaxe da função  pfss(). Na sequência são explicados os parâmetros de entrada da função.
  
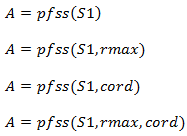Figura 8.
- S1: Um sistema linear dinâmico no estado-espaço ou a representação de uma função de transferência (que pode ser construida com a função syslin()).

- rmax: Um número real que controla o condicionamento da diagonalização do bloco (ver bdiag()).

-cord: Uma seqüência de caracteres com possíveis valores 'c' (para tempo contínuo) ou 'd ' (para tempo discreto).


Scripts testados com: Scilab 5.5.2 (64-bit)
                                       Scilab 6.0.0 (64-bit)*

 *Com esta versão, o programa da figura 6 construiu a função "E" (linha 0027), mas não executou a linha seguinte, que aplica a função  pfss() . 
Marcadores:
Local: Brasil

Comentários

Postar um comentário

Postagens mais visitadas deste blog

Critério de Estabilidade de Routh-Hurwitz

Critério de Estabilidade de Routh-Hurwitz Em uma outra postagem foi apresentado o critério de polos e zeros para verificar a estabilidade de um sistema. Na mesma linha de análise, temos também o critério de estabilidade de Routh-Hurwitz, que é explicado na sequência. O que é ? "Na teoria dos sistemas de controle , o critério de estabilidade de Routh-Hurwitz é um teste matemático que é uma condição necessária e suficiente para a estabilidade de um sistema de controle linear e invariante no tempo (LTI). O teste de Routh é um algoritmo recursivo eficiente que o matemático inglês Edward John Routh propôs em 1876 para determinar se todas as raízes do polinômio característico de um sistema linear apresentam partes reais negativas. O matemático alemão Adolf Hurwitz propôs de forma independente, em 1895, organizar os coeficientes do polinômio em uma matriz quadrada, chamada de matriz de Hurwitz, e mostrou que o polinômio é estável se, e somente se, a sequência dos determinantes de...
Postar um comentário
Leia mais

Função Degrau Unitário

Função Degrau Unitário O que é ? A função degrau unitário (ou função de Heaviside) é muito utilizada na disciplina de Sinais e Sistemas Lineares e em análise de circuitos elétricos. Normalmente esta função é representada pela letra "u", e é dependente do tempo. Para valores de tempo menor que 0, a função vale 0, já para valores maiores ou iguais a 0, ela vale 1.  Podendo ser representada Pra que serve ?  Podemos usar a função degrau unitário para limitar o intervalo de outra função. Se tivermos um sinal y(t), como mostrado abaixo Gráfico 1.  e quisermos que ele inicie-se no tempo zero, então y(t) deve ser multiplicada por u(t).  Gráfico 2. Outra aplicação é para a representação de certas funções em termos de u(t). Isso pode ser conseguido com a manipulação da variável independente, no caso o tempo, manipulação da função u(t) além da combinação de diferentes funções degrau. Alguns exemplos se encontram log...
Postar um comentário
Leia mais

Polos e Zeros - Função plzr()

Polos e Zeros O que é ? Figura 1. Antes de falarmos de polos e zeros, vamos começar pela definição de função de transferência (FT). Temos que, a FT de um sistema linear nada mais é do que a relação entre a transformada de Laplace   da variável de saída com a transformada de Laplace da variável de entrada. Vale lembrar que as condições iniciais devem ser zero.    Figura 2. A FT do sistema representado no diagrama da figura 1 é a função G(s) (figura 2), em que a variável s (minúsculo) é chamada de frequência complexa. S(s) e E(s) são polinômios. E(s) é chamado de polinômio característico do sistema, sendo o grau n-ésimo desse polinômio  a ordem do sistema. Agora vamos as definições de polos e zeros. Polos: S ão os valores de s, de E(s) de uma função de transferência, que fazem com que a FT se torne infinita . Em outras palavras, são as raízes de E(s) = 0  Zeros: São  os valores de s, de S(s) de uma função de transferência, que fazem com ...
Postar um comentário
Leia mais